▲遊戲本身基礎功能只有移動、轉向,無法直接輸出坐標得到絕對位置,導致難以畫出函數曲線,相比Scratch功能還是過少。我目前測試如何於武館中實現坐標系,且已經成功做出簡單的曲線圖形,以下是思路與成果介紹。
(註:白底與座標軸是一開始先畫好的,介紹中不會提及)
如果過程不太懂,可以去段落總結看圖抄下總積木。
(一)單一座標位移
1.基本位移例子
▲首先,假設角色初始位在(0,0)且面朝𝑥軸正向,我想從(0,0)移動到(40,80),我除了需要知道兩點間直線距離,還需要知道左轉角度θ。
註:為了方便,我會稱呼𝑑𝑥=(40-0),𝑑𝑦=(80-0),其中𝑑𝑥與𝑑𝑦分別是水平方向與鉛直方向的距離變化量。接著根據觀察可得知𝑑𝑦/𝑑𝑥其實就是斜率𝑚的定義,因此一樣為方便,取一變數𝑚=𝑑𝑦/𝑑𝑥。
三角函數: 正切函數tan(θ)=𝑚,反正切函數arctan(𝑚)=θ
▲接下來我令_X、_Y為我的目標座標。前者距離(distance)很容易,套用√ ((40-0)²+(80-0)²可解決,但後者轉向很麻煩,已知邊長,如何求角度?此時就要採用反三角函數,從邊長逆向推回角度θ,而其中使用arctan反正切函數最簡便,因為arctan需要的條件是𝑑𝑦/𝑑𝑥,這兩個值都是一開始已知的。
▲但遊戲沒有內建三角函數,我仍然選擇使用泰勒展開近似arctan,項數取越多就越準確。上圖在|𝑥|<1時可適用。
▲並且這次只取前幾項精度會不太夠,所以列出通式比較好。
▲上圖13579...函數使得𝑚1輸出arctan(𝑚)的泰勒展開前81項,並回傳𝑚1到arctan(𝑚)。理論上取越多項越好,但考慮電腦跑不動的問題,還是適當取就好。
注意,以上例子只在絕對值|𝑚|<1可用,為了之後的推廣,肯定不能只考慮這個情況。
▲在這裡我已經把𝑚的不同情況用邏輯積木劃分出來了。|𝑚|≥1時,輸進arctan的值為1/𝑚,加減π/2後回傳arctan。這裡更要注意的是,arctan的值是弧度量,因此最後的回傳值要經過運算×180÷𝝅換為度度量。
至此arctan函數已經完成。
註:這裡的𝝅我已經事先設定好變數值為3.141592653589793
▲把arctan轉為度度量的值並回傳後,就能得到這樣一條基本運算規則,並且我讓角色在移動到目標位置後重新轉回𝑥軸正向的位置。
▲這樣第一大挑戰就完成了。
2.推廣四象限
▲很快的,嘗試時會發現其他象限出錯,事情還沒有結束。
▼但要解決這個問題不難,並且方法可以在維基百科找到
▲可以新定義一個atan2函數,負責在象限不同時轉換arctan函數。
▲原函數arctan去掉度度量運算和函數參數中的𝑑𝑥,𝑑𝑦,並移植到新函數atan2裡。而atan2函數的換算就直接用圖片展示了。
▲記得把轉向的函數改為atan2。
▲這樣四個象限都能適用。
(二)多點圖形軌跡
1.多點直線軌跡
一開始我們假設原點(0,0),而目前我們在一次位移後的某點,比如(40,80),那就需要更新狀態▼。
▲讓𝑑𝑥與𝑑𝑦不再是(0,0)的位移變化量,而是當前位置的位移變化量。起始的座標(𝑥₀,𝑦₀)=(0,0),經過一次位移,起步的座標(𝑥₀,𝑦₀)=(40,80),以次類推。
▲只要輸入特定點座標,就能在路線上畫出幾何圖形。
▲可以透過邏輯判讀偵測不想畫的線段,比如設定函數的參數de,只要de的值是0,就會前跳而非前進。
2.多項式函數
▲給予𝑥、𝑦的關係式,就能畫出多項式函數,間隔越小越精確,但間距太小會花費過多時間執行,選擇取0.2~0.5差不多。這裡為了避免𝑑𝑦/𝑑𝑥出現除以0的情況,所以加了𝑥≠0的條件。
▲當畫出雙邊軌跡時察覺多了一條不想要的軌跡。
▲只使用𝑑𝑥正負判斷,畫𝑦=𝑥²等函數可行,畫𝑦²=𝑥等非函數就會出錯。因為我使用的迴圈從-20畫到20,畫函數時的𝑑𝑥保持為正,但非函數𝑦²=𝑥的𝑑𝑥會從正到負再到正,發生多出其他軌跡的情況。
(2025/03/06更新內文)
3.非函數圖形
▲解決非函數的方法與先前類似,只要為此類方程式再加一個檢查𝑑𝑦正負的判斷式就好。目前判斷一層套一層弄得有些混亂,經過修改後換成比較易懂的形式。de判斷改成顏色,判讀條件如上圖,想畫函數,de參數就輸入紅色;想畫圖中的非函數拋物線𝑦²=-25𝑥,de就輸入綠色。
▲𝑥與𝑦座標的關係式以上圖為例,座標𝑥=-x²,座標𝑦=5x,移項可以得到x=(𝑦/5),帶入第一式的x得出𝑥=-(𝑦/5)²,再移項即是結果𝑦²=-25𝑥。
避免混淆,迴圈變數x改為t。
----------------------------------------------------------------
段落總結:
一、初始變數
二、四大函數
(1)
▲上圖代表反正切函數於𝑥=0的泰勒展開,n取越多項越精準,考慮電腦性能與執行速度可減少上圖81項到可負擔的程度。迴圈未給數值時,範圍視為0,間隔視為1。
▲收合積木的展開如上。
▲中間那項1.3.5是一變數,^是次方。
(2)
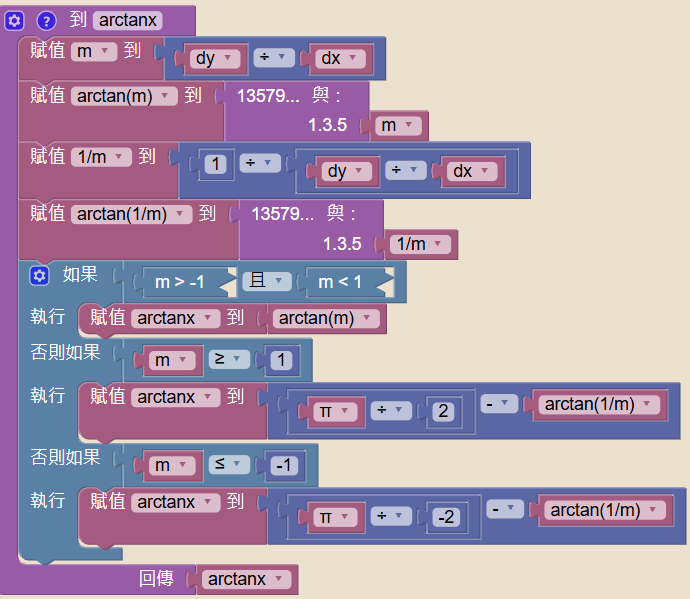
▲反正切函數,回傳弧度量數值,不需動。
▲反正切函數,回傳弧度量數值,不需動。
(3)
▲反正切函數的四象限判讀函數,回傳度度量數值,不需動。
(4)
▲總函數,決定能畫出的函數種類,調整的重點。
三、函數繪製
繪製條件:
▶𝑥,𝑦等於座標點,定中心為(0,0)
▶一律無軌跡:de=白(#ffffff)
▶一律有軌跡:de=黑(#000000)
▶畫函數:de=紅(#ff0000)
▶畫非函數:de=綠(#33ff33)
四大函數建立好後,可選擇直接定位到特定座標點▼,或者畫多項式函數。
▲一般座標方形範例。
▲畫多項式函數,其中𝑥,𝑦的關係式以上圖為例運算為:
𝑥=10𝑡 ⇒ 𝑡=(𝑥/10)
𝑦=-𝑡² ⇒ 𝑦=-(𝑥/10)²
⇒ 𝑦=(-1/100)𝑥²
方程式對應武館400×400單位的空間。以上其實就是參數式轉換為一般函數形式的過程,如果參數式寫成:
𝑥=𝑡
𝑦=(-1/100)𝑡²
能更直觀看出函數的形式,後續文章會介紹。
▲目前可以畫出來的各種函數或其他曲線。
未來繪圖目標:
雙曲線(3/7已完成)
指對數(3/8已完成)
三角函數(3/8正弦、餘弦已完成)
圓(3/8已完成)
橢圓(3/8已完成)
武館連結(需登入E-game帳號才可見):
相關文章:
個人武館: